株式会社エム・イー・エル Microwave & Electronics Laboratory
一口講座 スミスチャートの基礎 小川隆博 著を拝見して、
エクセルによるスミスチャート作画実験中です。
試行錯誤な状態ですので未完成です。
Smithchart.xls サイズ=1.56 MB (1,639,936 バイト)のダウンロード
グラフ目盛りの計算式を抜いたシンプル版(2011年1月21日)もアップしました
当方は使用によって生じた損害等の一切保障および責任を負いません。
利用者の自己責任においてご利用ください。
スミスチャートの利用例として ★エクセルを使ったLPF、HPFシミレーション★も御覧ください。
ご感想・ご意見・ご要望・バグなどございましたら、
下記までご連絡いただけましたら幸いです。
hide096096あyahoo.co.jp あ=@に置き換えてください。
【YouTube】に動画をアップしました。デモ手動データ入力なので遅いですが、
セルにデータが入っていれば瞬時で、もっと速いです。
【スミスチャートYouTube】
【アドミッタンスチャートYouTube】
【イミッタンスチャートYouTube】
【プロットYouTube】
【負性抵抗YouTube】勉強中 011/01/18 ×××間違いでした×××
2011/01/19 等角写像にしたがっていれば
表現方法としては間違いではなさそうです。
【負性抵抗YouTube】勉強中 2
r=-0.5〜r=-2の間は1部しか表現できていませんので不完全。
【負性抵抗YouTube】勉強中 3
R≒0近傍がプロットできるみたいだけど利用価値は???。
エクセル スミスチャート・円と円の交点
r1(X,0) r2(1,Y) r2=Yにすると計算式が少しシンプルになります。
r1(0,0) r2(1,Y) r2=Yにすると計算式がよりシンプルになります。
★★★★★★★★★★★ ただいま勉強中 ★★★★★★★★★★★★★★★★★
★2011/01/18 やっぱり大きな勘違いでした。
★最下部に追記しました。またここに戻ってきます。(試行錯誤)
↓↓↓↓↓↓↓↓↓↓↓ 011/01/19追記 ↓↓↓↓↓↓↓↓↓↓↓
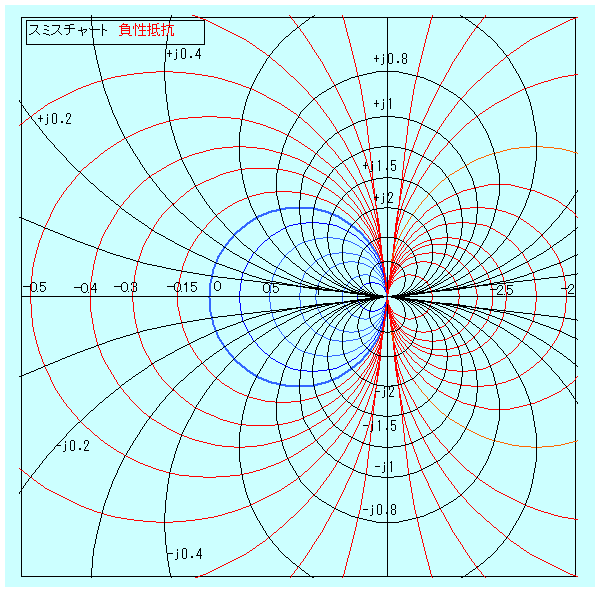
図1や図2でr=-1近傍の再考察をして見ました。
図4では|Γ|=1の円はよく分かりませんでしたが、
等角写像(Wikipedia)にしたがって−R〜−∞の領域(右側橙色円)は
>原点からr/(r+1)だけ移動
>円の半径は、1/(r+1)・・・・・
これにオフセットと符号を細工してよいかどうか検証中です。
Γx=COS(n/N*2*PI())/(-r+1)+2-(-r/(-r+1))
Γy=SIN(n/N*2*PI())/(-r+1)
多分この目盛りの式と同じ式でデータープロットすればよいかな?
±0近傍であればR=−0.4図かR=−0.5図
マイナス側全領域を表現するならばR=−0.0図がよいような・・・
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
一口講座 スミスチャートの基礎の
「図 4 負性抵抗領域まで表わしたスミスチャート」は、
下図のようになっているように思えました。(私の勝手な想像解釈です)
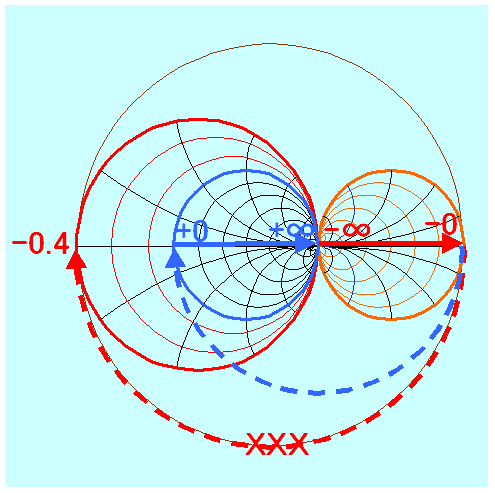
青点線はなんとなく納得ですが、
赤点線はつじつまが合わないような気がします。
負性抵抗領域はチンプンカンプンです。
>原点からr/(r+1)だけ移動
>円の半径は、1/(r+1)・・・・・
この式を使ってエクセル作画を試行錯誤中です。
負の領域は巨大な円になると思うので、
ある部分(R=-0.5)からベクトルを+∞の右側にあると考えてみました。
紫色の範囲が同じベクトル量だと思っています。
現在アップロードしてあるエクセルファイルはR=−0.5〜-0.0用ですので
それぞれ表示領域によってグラフオプションで数値軸(x、y)をオンにして、
数値軸目盛(最小値、最大値)を変更したほうがよいでしょう。
−25Ω〜+50Ω位用
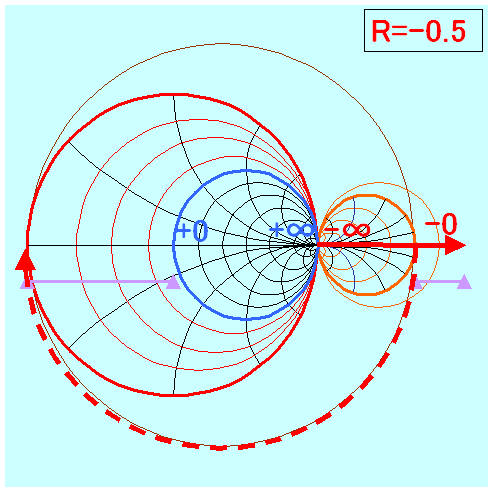
−20Ω〜+50Ω位用
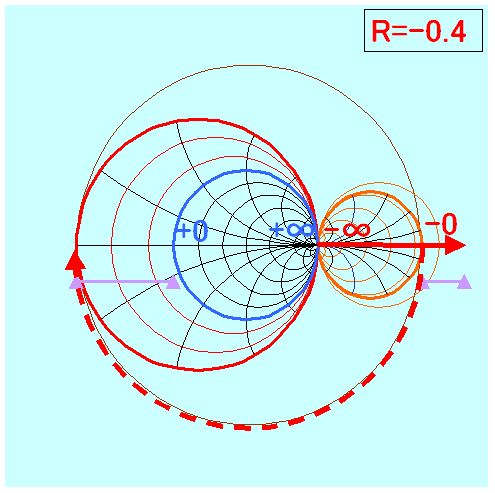
−15Ω〜+50Ω位用
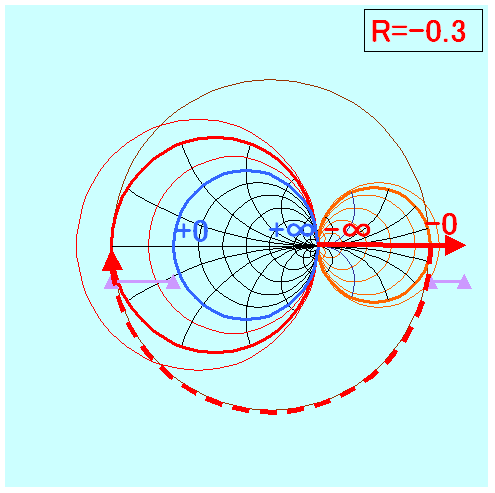
−10Ω〜+50Ω位用
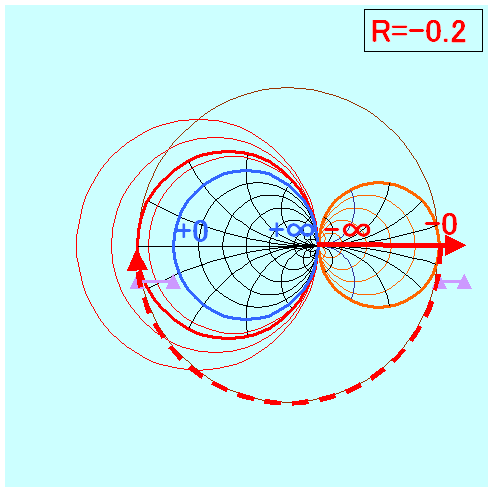
±全領域用
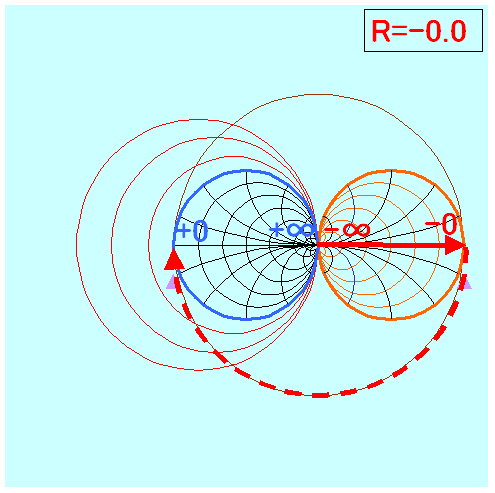
上記をパラパラ漫画にすると、
(R=-0.5)か(R=-0.4)が0付近の作画しやすそうです。
しかし、この考え方でよいかどうか自身がもてません。
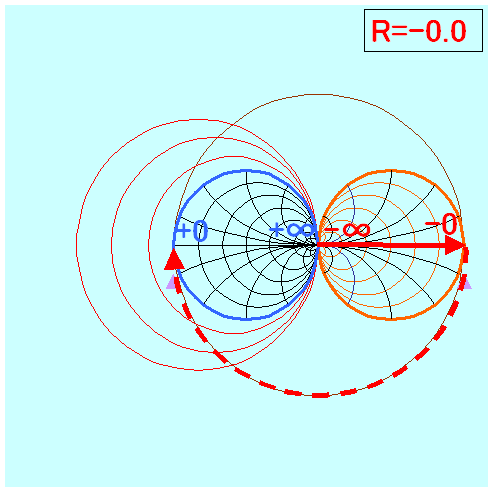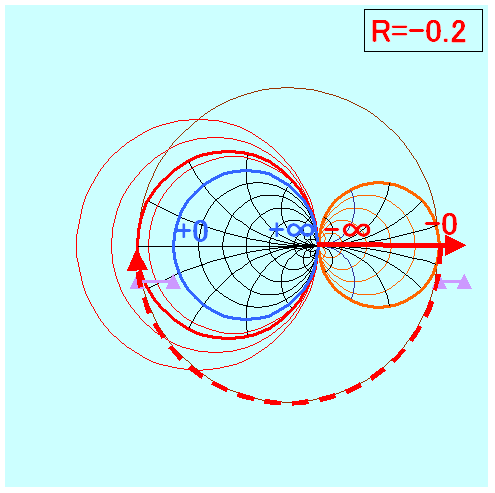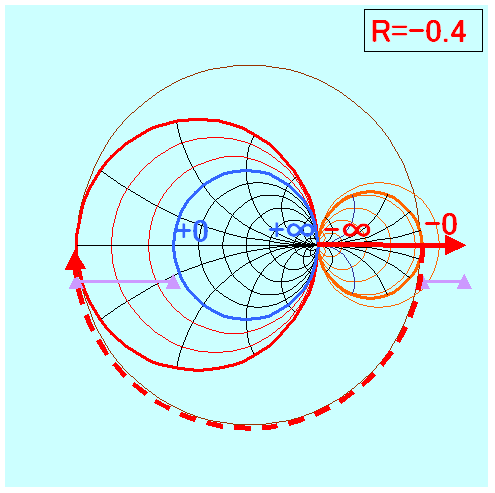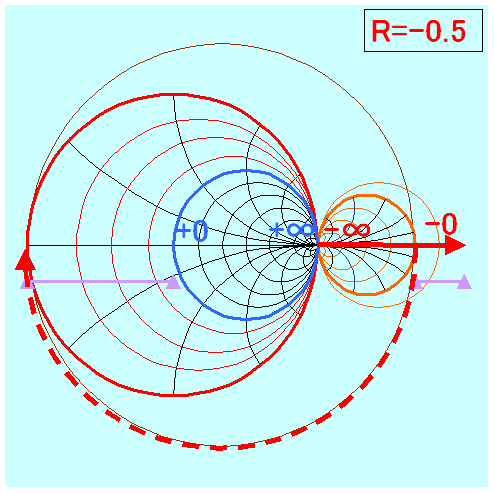
★2011/01/18 やっぱり大きな勘違いでした。
r=-1近傍を考察しなおしたらつじつまが合うようです。(数式どおり)
r=-0.5〜r=-2の間は1部しか表現できていません。
チョッと進歩したような気がします。
しかしスマートじゃないな・・・
2011/01/19
小川様よりご指導いただき
>あまり円の式にとらわれずに、
>等角写像にしたがって忠実に軌跡を描けばRの正負に関係なくチャートができると思います。
ということのようです。元に返ります。↑(試行錯誤)